1.
MEDIDAS DE
TENDENCIA CENTRAL
- Media aritmética: Se calcula para variables cuantitativas y se trata del centro
geométrico o de gravedad de nuestros datos. Es la suma de todos los valores de
la variable observada entre el total de observaciones. La fórmula es:
x= Ʃx/n
- Mediana: medida de posición y central.Es el valor de la
observación tal que deja a un 50% de los datos
menor y otro 50% de los datos mayor.
-
Si
el número de observaciones es impar el
valor de la observación será justamente la observación que ocupa la posición (n+1/2)
Ejemplo: si son 75, pues 76 entre 2 = 38, la mediana seria la edad que tiene el
sujeto 38.
-
Si
el número de observaciones es par,
el valor de la mediana corresponde a la media entre los dos valores centrales,
es decir, la media entre la observación n/2 y la observación (n/2)+1. Ejemplo:
cuatro sujetos de edades, 10, 15, 20, 25, cogemos los dos sujetos centrales y
hacemos la media aritmética entre ambos.
- Propiedad: robustez. Sólo tiene en cuenta la posición de los valores en la muestra y por tanto tiene mucho mejor comportamiento que la media cuando hay observaciones extremas.
- Moda: Es el valor con mayor frecuencia (que más veces se repite). Si hay más de una se dice que la muestra es bimodal (dos modas) o multimodal (más de dos modas). Se puede calcular para cualquier tipo de variable tanto la cualitativa como la cuantitativa. La moda no es el número más frecuente si no la categoría.
Si los datos están agrupados, se habla de clase modal y corresponde al intervalo
en el que el cociente entre la frecuencia relativa y la amplitud (se resta el
intervalo mayor menos el menor) es mayor (hi/ci). Donde
la frecuencia absoluta sea mayor.
2.
MEDIDAS DE POSICIÓN O CUANTILES
Se calculan para
variables cuantitativas y, al igual
que la mediana, sólo tienen en cuenta la posición
ordenado de mayor o menor de los valores en la muestra.
Los cuantiles más
usuales son los percentiles, los deciles y los cuartiles, según dividan la muestra ordenada en 100 (perciles), 10
(deciles) ó 4 partes (cuartiles), respectivamente.
-
Percentiles:
o
Dividen
la muestra ordenada en 100 partes.
o
El
percentil “i” (Pi), es aquél valor que, ordenadas las observaciones
en forma creciente, el i% de ellas son menores que él y el (100-i)% restante
son mayores.
o
Para
buscar la posición de un percentil en una serie de datos agrupados, buscamos el
intervalo en el que la frecuencia relativa acumulada (Hi) sea
superior al valor del percentil.
o
El
valor del P50 corresponde al valor de la mediana.
-
Deciles:
o
Dividen
la muestra ordenada en 10 partes.
o
El
decil “i” (Di), es aquél valor que, ordenadas las observaciones en
forma creciente, el i/10% de ellas son menores que él y el (100-i)/10% restante
son mayores.
o
El
valor del D5 corresponde al valor de la mediana y, por tanto, al del
P50.
-
Cuartil:
o
Dividen
la muestra ordenada en 4 partes.
o
El
Q1, primer cuartil indica el valor que ocupa una posición en la
serie numérica de forma que el 25% de las observaciones son menores y que el
75% son mayores.
o
El
Q2, segundo cuartil indica el valor que ocupa una posición en la
serie numérica de forma que el 50% de las observaciones son menores y que el
50% son mayores. Por tanto, el Q2 coincide con el valor del D5,
con el valor de la mediana P50.
o
El
Q3, tercer cuartil indica el valor que ocupa una posición en la
serie numérica de forma que el 75% de las observaciones son menores y que el
25% son mayores.
o
El
Q4, cuarto cuartil indica el valor mayor que se alcanza en la serie
numérica.
3. MEDIDAS DE DISPERSIÓN.
- Rango o recorrido: Diferencia entre el mayor y el menor valor de
la muestra lXn-X1l (valor absoluto).
-
Desviación media: Media aritmética de las distancias de cada observación con respecto a la
media de la muestra:
Para datos agrupados:
-
Desviación típica o estándar: Cuantifica el error que ometemos si
representamos una muestra únicamente por su media. Esta es la que más se emplea debido a que esta
nos da un mayor rango de error.
Para datos agrupados:
- Varianza: Expresa la misma información en valores cuadráticos:
Para agrupados:
- Recorrido intercuartílico: Diferencia entre el tercer y el primer
cuartil = lQ3-Q1l
- Coeficiente de variación: Es una medida de dispersión relativa
(adimensional) ya que todas las demás se expresan en la unidad de medida de la
variable. Nos sirve para comparar la heterogeneidad de dos series numéricas con
independencia de las unidades de medidas. Se expresa sin unidades. Siempre va de 0 a 1.
- c.v.=s/x
4. DISTRIBUCIONES NORMALES
En estadística se llama distribución normal, distribución de
Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de
variable continua que con más frecuencia aparece en fenómenos reales. Es
Distribución de probabilidad más frecuente con variables continuas, por
ejemplo, altura, peso, niveles de colesterol…
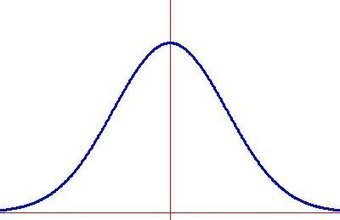
Las distribuciones normales en un histograma aparece una
especie de Campana, por eso la campana de Gauss. Y es simétrica respecto de los
valores de posición central, es decir que la moda va a coincidir con la media y
la mediana.
|
Media, moda, mediana.
|

Una distribución normal sigue estos principios
básicos: si al valor de la media le restamos y le sumamos una desviación
típica, si la serie numérica siguiera una distribución normal (como el
colesterol). Dice que el 68.25% de las observaciones se va a sumar entre los
valores de la suma y la resta de la media a una desviación típica. Estas datos
varían si sumamos una, dos o tres desviaciones típicas.
-
S
68,26% de las observaciones.
-
2xS95,45% de las observaciones.
-
3xS 99,73% de las observaciones.
5.
ASIMETRÍAS Y CURTOSIS
La asimetría
es al lado contrario al que vemos el pico (la moda), es decir si vemos el pico
hacia la derecha la asimetría es a la izquierda, y si la moda esta a la
izquierda la asimetría esta hacia la derecha.
Coeficiente de asimetría de una
variable: Grado de asimetría de la distribución de sus datos en
torno a su media, cuanto más asimétrica sea, valores más diferentes
encontraremos.
- Asimetrías:
Los
resultados pueden ser los siguientes:
-
g1=0 (distribución simétrica; existe la
misma concentración de valores a la derecha y a la izquierda de la media).
-
g1>0 (distribución asimétrica positiva;
existe mayor concentración de valores a
la derecha de la media que a su izquierda).
-
g1<0 (distribución asimétrica negativa;
existe mayor concentración de valores a la izquierda de la media que a su
derecha).
- Curtosis o
apuntamiento de la curva:
No tiene
relación con la simetría. Coeficiente de apuntamiento o curtosis de una
variable, sirve para medir el grado de concentración de los valores que toma en
torno a su media. Los datos se acumulan mucho, mientras más se acumulen, mas
apuntada esta la curva.
Los
resultados pueden ser los siguientes:
-
g2=0
(distribución mesocúrtica o normal). Presenta un grado de concentración medio
alrededor de los valores centrales de la variable (el mismo que presenta una
distribución normal).
-
g2>0
(distribución leptocúrtica). Presenta un elevado grado de concentración
alrededor de los valores centrales de la variable.
-
g2<0
(distribución platicúrtica). Presenta un reducido grado de concentración
alrededor de los valores centrales de la variable.
6.
TIPICACION DE LOS VALORES Y SU
RELACION CON LA CAMPANA DE GAUSS.
Trabajamos
con una variable continua que:
-
Sigue
una distribución normal (TLC)
-
Tiene
mas de 100 unidades (LGN)
La tipificación nos permite conocer si valor
corresponde o no a esa distribución con frecuencia

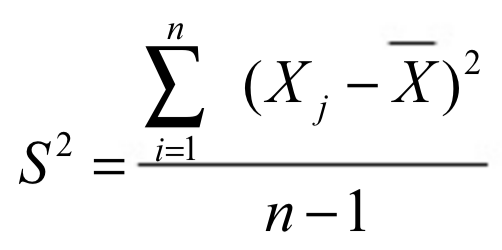


No hay comentarios:
Publicar un comentario